広島文理科大学波動幾何学研究所

自然哲論お勉強会

応援いただけましたら励みになります（・ω・）ノシ

角運動量２～面積速度一定の法則～

やっと発表が終わりました（＾▽＾）
まわりの若い子はホント優秀で、みんなＤ１にして単位そろえかねない。
一方のこちらはマイペース、マイペースじゃ～と自分で呪文を唱えないと精神が保たれません（；ω；）

さておき、４０代からの量子力学、再開いたしますじゃ。

wave-geometry.hatenablog.com

前回は慣性モーメントをえるところまで行ったんですね…。

${L=I\omega,\ \ \ I = mr^2}$

イナーシャについては、「面積、質量×面積だ…」と呪文を唱えればいいでしょう（謎）。

今回は古典論の枠組みの中で、角運動量の成分を解析いたします。

まず、 ${\omega=v/r}$ をリコール。
↓ここで導出したやつですじゃ。
wave-geometry.hatenablog.com

これと上の慣性モーメントの式から、

${L=I\omega=mr^2\displaystyle\frac{v}{r}}$

${=mrv}$

${p=mv}$ なので、最終的には

${L=rmv=rp}$

に落ち着きまする。

さて、ここでさらなる分析のために、ケプラーの第２法則と呼ばれる物理法則を用います。
惑星惑星してそうで、心が躍りますな。

f:id:morio_roji1111:20180601202757p:plain

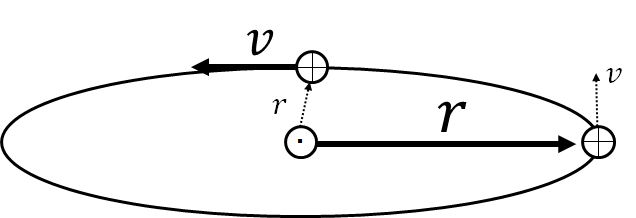
中央の点は太陽、楕円軌道上の丸にジュノジは地球であります。
${r}$ は半径、 ${v}$ は速度で、どちらもベクトルだと思っていただきたいのであります。

何を申し上げたいのかといいますと、地球が太陽に近いところでは勢いよく通り過ぎるんですが、遠く離れると勢いは弱まってるんですな。
中心力のなせる業…ですかいのう？

そういうわけで、 ${\bf{\it{r}}\cdot \bf{\it{v}}}$ の関係は常に一定、保存しておるのです。

これを「面積速度一定の法則」というようです…イコール第２法則なのですかな。
ですな。

よって「面積速度＝角運動量は保存する」を確かめて利用すれば良い…という寸法じゃ。

さて。

f:id:morio_roji1111:20180601203359p:plain

半径が大きくないと感じにくいですが、かなり大きくなると、円周の部分を直線で近似して、図のように三角形を見出すことができます。

ここから、以下の関係を得るのですな。

${求める面積=\displaystyle\frac{1}{2}\times rv\sin{\theta}}$

... ${\cos{\theta}}$ ではないのんね？
そう、ないのです。
そこで、良く知ってるベクトルとコサインの関係、

${\mathbf{r\cdot v}=rv\cos{\theta}}$

に当てはめるためには、一工夫必要なのですな。
まず、

${\mathbf{r}= \left( \begin{array}{r} x \\ y \\ \end{array} \right) ,\ \ \ \mathbf{v}= \left( \begin{array}{r} v_x \\ v_y \\ \end{array} \right) }$

とおきますだ。

${\sin\theta}=\sqrt{1-\cos^2{\theta}}$

${rv \sin\theta}=rv \sqrt{1-\displaystyle(\frac{\mathbf{r\cdot v}}{rv})^2}$

${rv\sin\theta}=\sqrt{r^2v^2-\displaystyle r^2v^2 (\frac{\mathbf{r\cdot v}}{rv})^2}$

${rv\sin\theta}=\sqrt{r^2v^2-(\mathbf{r\cdot v})^2}$

${rv\sin\theta}=\sqrt{\left( \begin{array}{r} x \\ y \\ \end{array} \right) ^2 \left( \begin{array}{r} v_x \\ v_y \\ \end{array} \right) ^2 - (\mathbf{\left( \begin{array}{r} x \\ y \\ \end{array} \right) \cdot \left( \begin{array}{r} v_x \\ v_y \\ \end{array} \right) })^2}$

${rv\sin\theta}=\sqrt{(x^2+y^2)(v_x^2+v_y^2)-(xv_x+yv_y)^2}$

${rv\sin\theta}=\sqrt{x^2v_x^2+x^2v_y^2+y^2v_x^2+y^2v_y^2-(x^2v_x^2+2xv_y yv_x+y^2v_y^2)}$

消える項を整理しますと、

${rv\sin\theta}=\sqrt{x^2v_y^2-2xv_y yv_x+y^2v_x^2}$

${rv\sin\theta}=\sqrt{(xv_y-yv_x)^2}$

よしよし、でましたな！
求めてきた面積速度＝角運動量とやらは、

${rv\sin\theta=|xv_y-yv_x|}$

に落ち着きましただ。

ここで最初の角運動量の式 ${L=rmv=rp}$ より、

${L=m|xv_y-yv_x|}$

${p=mv}$ より、

${L=xp_y-yp_x}$

…ちなみにこの ${L}$ は、 ${xy}$ 面内の運動に対する外積なので ${z}$ 方向、
すなわち

${L_z=xp_y-yp_x}$

なのであります。

（続く）
~~~~~~~~~~~~~~~~~~
↓応援いただけましたら励みになります（・ω・）ノシ