2018-07-09

經Delta函數描寫Coulomb互相作用

${x(r,t)}$ .

${v(x-x')=v(r-r')\delta(t-t')}$

意思就是主觀在 ${r}$ ，作用對象在 ${r’}$ ．
但是作用只能生起於 ${t-t'}$ 的須臾之間．

...話以後擴張到Green函數．
因它會描寫按照time ordering的現象...

2018-07-08

シュレーディンガー方程式を解く2

第2回ですじゃ．

前回はラプラシアンの中身を作るところの出だしまででしただ．

${\displaystyle\frac{\partial r}{\partial x}=\frac{x}{r}=\sin{\theta}\cos{\phi}}$

この調子だと，他の変数についてもいけそうだなや！

${\displaystyle\frac{\partial r}{\partial y}=\frac{y}{r}=\sin{\theta}\sin{\phi}}$

${\displaystyle\frac{\partial r}{\partial z}=\frac{z}{r}=\cos{\theta}}$

よしよし．

それでは次は ${\theta}$ ．

${\displaystyle\frac{\partial}{\partial x}=\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta}}$

前回の(3)でarctanにしちゃってるけど，

${\tan^{2}{\theta}=\displaystyle\frac{x^2+y^2}{z^2}}$

こいつを使いましょうぞ．

${\displaystyle\frac{\partial}{\partial x}\displaystyle\frac{x^2+y^2}{z^2}=\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta}\tan^{2}{\theta}}$

${\displaystyle\frac{\partial}{\partial x}\displaystyle\frac{1}{z^2}\cdot(x^2+y^2)=\frac{\partial\theta}{\partial x}\frac{2\tan{\theta}}{\cos^2{\theta}}}$

${\displaystyle\frac{2x}{z^2}=\frac{\partial\theta}{\partial x}\frac{2\tan{\theta}}{\cos^2{\theta}}}$

関数の積の微分，前々回の結果など使いました．

wave-geometry.hatenablog.com

式を整理します．

${\displaystyle\frac{\partial\theta}{\partial x}=\frac{x}{z^2}\frac{\cos^2{\theta}}{\tan{\theta}}}$

${\displaystyle\frac{1}{\tan{\theta}}=\displaystyle\frac{\cos{\theta}}{\sin{\theta}}}$ だし，

${\cos{\theta}=\displaystyle\frac{z}{r}}$ だし，

${x=r\sin{\theta}\cos{\phi}}$ だしで，

${\displaystyle\frac{\partial\theta}{\partial x}=\frac{r\sin{\theta}\cos{\phi}}{z^2}\frac{z^2}{r^2}\frac{\cos{\theta}}{\sin{\theta}}}$

${\displaystyle\frac{\partial\theta}{\partial x}=\frac{1}{r}\cos{\theta}\cos{\phi}}$

次はy，

${\displaystyle\frac{2y}{z^2}=\frac{\partial\theta}{\partial y}\frac{2\tan{\theta}}{\cos^2{\theta}}}$

${\displaystyle\frac{\partial\theta}{\partial y}=\frac{y}{z^2}\frac{\cos^2{\theta}}{\tan{\theta}}}$

${\displaystyle\frac{\partial\theta}{\partial y}=\frac{r\sin{\theta}\sin{\phi}}{z^2}\frac{z^2}{r^2}\frac{\cos{\theta}}{\sin{\theta}}}$

${\displaystyle\frac{\partial\theta}{\partial y}=\frac{1}{r}\cos{\theta}\sin{\phi}}$

${\theta}$ の最後はz，これはちょっとだけ違う．

${\displaystyle\frac{\partial}{\partial z}\left\{z^{-2}(x^2+y^2)\right\}=\frac{\partial\theta}{\partial z}\frac{2\tan{\theta}}{\cos^2{\theta}}}$

${\displaystyle\frac{-2(x^2+y^2)}{z^3}=\frac{\partial\theta}{\partial z}\frac{2\tan{\theta}}{\cos^2{\theta}}}$

${\displaystyle\frac{\partial\theta}{\partial z}=\frac{-(x^2+y^2)}{z^3}\frac{\cos^2{\theta}}{\tan{\theta}}}$

${\displaystyle=-\frac{r^2\sin^2{\theta}}{r^3\cos^{3}{\theta}}\frac{\cos^3{\theta}}{\sin{\theta}}}$

${\displaystyle=-\frac{1}{r}\sin{\theta}}$

これで ${\theta}$ の段は出揃いましただな．

${\displaystyle\frac{\partial\theta}{\partial x}=\frac{1}{r}\cos{\theta}\cos{\phi}}$

${\displaystyle\frac{\partial\theta}{\partial y}=\frac{1}{r}\cos{\theta}\sin{\phi}}$

${\displaystyle\frac{\partial\theta}{\partial z}=-\frac{1}{r}\sin{\theta}}$

次は ${\phi}$ の段．
（・〜・）がんばりますだ．

${\tan{\phi}=\displaystyle\frac{y}{x}\cdots(1)}$ を使いますのじゃ．

まずはx，

${\displaystyle\frac{\partial}{\partial x}\left(\frac{1}{x}\cdot y\right)=\frac{\partial\phi}{\partial x}\frac{1}{\cos^2{\phi}}}$

${-\displaystyle\frac{y}{x^2}=\frac{\partial\phi}{\partial x}\frac{1}{\cos^2{\phi}}}$

${\displaystyle\frac{\partial\phi}{\partial x}=-\cos^2{\phi}\frac{r\sin{\theta}\sin{\phi}}{r^2\sin^2{\theta}\cos^2{\phi}}}$

${\displaystyle=-\frac{\sin{\phi}}{r\sin{\theta}}}$

次はy，

${\displaystyle\frac{\partial}{\partial y}\left(\frac{1}{x}\cdot y\right)=\frac{\partial\phi}{\partial y}\frac{1}{\cos^2{\phi}}}$

${\displaystyle\frac{1}{x}=\frac{\partial\phi}{\partial x}\frac{1}{\cos^2{\phi}}}$

${\displaystyle\frac{\partial\phi}{\partial y}=\frac{\cos^2{\phi}}{r\sin{\theta}\cos{\phi}}}$

${\displaystyle=\frac{\cos{\phi}}{r\sin{\theta}}}$

最後に，zは(1)の右辺がゼロになるんで，どうあってもゼロですだなぁ．

${\displaystyle\frac{\partial}{\partial z}\left(\frac{1}{x}\cdot y\right)=\frac{\partial\phi}{\partial z}\frac{1}{\cos^2{\phi}}}$

${\displaystyle\frac{\partial\phi}{\partial z}=0}$

（・∀・）ヨシヨシ．

まとめますと，

${\displaystyle\frac{\partial r}{\partial x}=\sin{\theta}\cos{\phi}}$

${\displaystyle\frac{\partial r}{\partial y}=\sin{\theta}\sin{\phi}}$

${\displaystyle\frac{\partial r}{\partial z}=\cos{\theta}}$

${\displaystyle\frac{\partial\theta}{\partial x}=\frac{1}{r}\cos{\theta}\cos{\phi}}$

${\displaystyle\frac{\partial\theta}{\partial y}=\frac{1}{r}\cos{\theta}\sin{\phi}}$

${\displaystyle\frac{\partial\theta}{\partial z}=-\frac{1}{r}\sin{\theta}}$

${\displaystyle\frac{\partial\phi}{\partial x}=-\frac{\sin{\phi}}{r\sin{\theta}}}$

${\displaystyle\frac{\partial\phi}{\partial y}=\frac{\cos{\phi}}{r\sin{\theta}}}$

${\displaystyle\frac{\partial\phi}{\partial z}=0}$

得られたこれらを，以下の式に代入すればよいのですじゃ．

${\displaystyle\frac{\partial}{\partial x}=\frac{\partial r}{\partial x}\frac{\partial}{\partial r}+\frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial x}\frac{\partial}{\partial \phi}}$

${\displaystyle\frac{\partial}{\partial y}=\frac{\partial r}{\partial y}\frac{\partial}{\partial r}+\frac{\partial \theta}{\partial y}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial y}\frac{\partial}{\partial \phi}}$

${\displaystyle\frac{\partial}{\partial z}=\frac{\partial r}{\partial z}\frac{\partial}{\partial r}+\frac{\partial \theta}{\partial z}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial z}\frac{\partial}{\partial \phi}}$

それっ，

${\displaystyle\frac{\partial}{\partial x}=\sin{\theta}\cos{\phi}\frac{\partial}{\partial r}+\frac{1}{r}\cos{\theta}\cos{\phi}\frac{\partial}{\partial \theta}-\frac{\sin{\phi}}{r\sin{\theta}}\frac{\partial}{\partial \phi}}$

${\displaystyle\frac{\partial}{\partial y}=\sin{\theta}\sin{\phi}\frac{\partial}{\partial r}+\frac{1}{r}\cos{\theta}\sin{\phi}\frac{\partial}{\partial \theta}+\frac{\cos{\phi}}{r\sin{\theta}}\frac{\partial}{\partial \phi}}$

${\displaystyle\frac{\partial}{\partial z}=\cos{\theta}\frac{\partial}{\partial r}-\frac{1}{r}\sin{\theta}\frac{\partial}{\partial \theta}}$

（；ω；）感涙
今回はここまで！

2018-07-07

シュレーディンガー方程式を解く

唐突に始まりました。
夏休みだからではありません。
台湾の研究所に夏休みはありません( ﾉД`)

それではスタート。
まずは極座標変換からです。

f:id:morio_roji1111:20180706212924p:plain

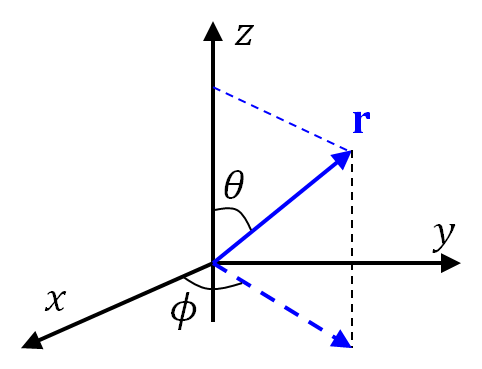
ちなみにθは天頂角と言います。Zenith angleです。
スクエアのフロントミッションを思い出してはいけません。
水平方向から登ればelevation angle、Φはazimuth angle、方位角です。

これらをデカルト座標x,y,zから、極座標r,θ,φに変換したいのです。
ここで、

${x=r\sin{\theta}\cos{\phi}}$
${y=r\sin{\theta}\sin{\phi}\cdots(1)}$
${z=r\cos{\theta}}$

の関係があります。

さて、シュレーディンガー方程式について、前回形を求めたことがありますんだ。

wave-geometry.hatenablog.com

${\left[\displaystyle - \frac{\hbar^2}{2m}\nabla^2+V(x)\right]\psi(x)=E\psi(x)}$

このなぶらさんですが、ベクトルの内積でして、

${\nabla^2=\nabla\cdot\nabla=\displaystyle\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\cdots(2)}$

こうなってます。

さあ、まずはこいつらから ${(x,y,z)\to(r,\theta,\phi)}$ するんずら。

…実はグランドクロス方程式（超謎）と余因子行列で作る逆行列を掛けるやり方でやったんだけど，
行列要素のとりかたの解釈で，ものすごいクリアに理解できたわけじゃなかったので，あえて背伸びして別のやり方しますだ．
（こっちのほうがきっとスマァトなんだ）

ではいきます．
(1)から，これを ${r,\theta,\phi}$ について解きます．

${r=\sqrt{x^2+y^2+z^2}}$
${\theta=\arctan{\displaystyle\frac{\sqrt{x^2+y^2}}{z}}\cdots(3)}$
${\phi=\arctan{\displaystyle\frac{y}{x}}}$

こんなかんじで．
arctanは図を見たりせんで，(1)の式から ${\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}}$ とかが取り出せそうな形に持ち込んで，うりゃあ（泣）とやります．

(2)のような，x,y,z偏微分に持ち込むために，以下のようにチェインルールとやらを使って考えます．

${\displaystyle\frac{\partial}{\partial x}=\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta}}$

こんな感じ．
この左右両辺は同じ作用をします．

これを(3)のrの式に作用させてみましょうえ．

${\displaystyle\frac{\partial}{\partial x}(x^2+y^2+z^2)^{1/2}=\frac{\partial r}{\partial x}\frac{\partial}{\partial r}r}$

${\displaystyle\frac{1}{2}(x^2+y^2+z^2)^{-1/2}2x=\frac{\partial r}{\partial x}}$

右辺のrは消えましただな．

${\displaystyle\frac{x}{\sqrt{x^2+y^2+z^2}}=\frac{\partial r}{\partial x}}$

${\displaystyle\frac{x}{r}=\frac{\partial r}{\partial x}}$

左右入れ替えて見やすくしますと，

${\displaystyle\frac{\partial r}{\partial x}=\frac{x}{r}=\sin{\theta}\cos{\phi}}$

よし，この調子で，

${\displaystyle\frac{\partial}{\partial x}=\sin{\theta}\cos{\phi}\frac{\partial}{\partial r}+\frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial x}\frac{\partial}{\partial \phi}}$

こういう式を作りましょうぞ！
（・∀・）

2018-07-06

分数関数の微分は関数の積の微分でイケる

なにがどうあってこんなところまで迷走したのか，いまとなってはさっぱりです．

${\left(\tan^2\theta\right)'=2\tan\theta\cdot(\tan\theta)'}$

${=2\tan\theta\cdot\left(\displaystyle\frac{\sin\theta}{\cos\theta}\right)'}$

この，最後の微分カッコの中身ですだな！
関数の積の公式， ${(fg)'=f'g+fg'}$ だけでいってみましょうえ．
楽しく!
（・∀・）

${\left(\displaystyle\frac{\sin\theta}{\cos\theta}\right)'=(\sin\theta)'\displaystyle\frac{1}{\cos\theta}+\sin\theta\left(\displaystyle\frac{1}{\cos\theta}\right)'}$